Time-domain THz Spectroscopy
The THz Regime
The THz wavelength regime encompasses the far- to mid-infrared range of about 0.1-100 THz, or about 3-3300 cm-1. Ultrafast THz sources rely on frequency conversion from the near-infrared (typically, 800 nm femtosecond pulses output by Ti:Sapphire lasers) into few- or single-cycle pulses.
The THz regime is especially interesting for condensed matter physics. This is the energy scale (0.4-400 meV) of many collective processes, like phonon and magnetic modes, superconducting gaps, and spin and charge ordering gaps, to name a few. It's also the energy scale of surface states in topological insulators and the Dirac cones of graphene.
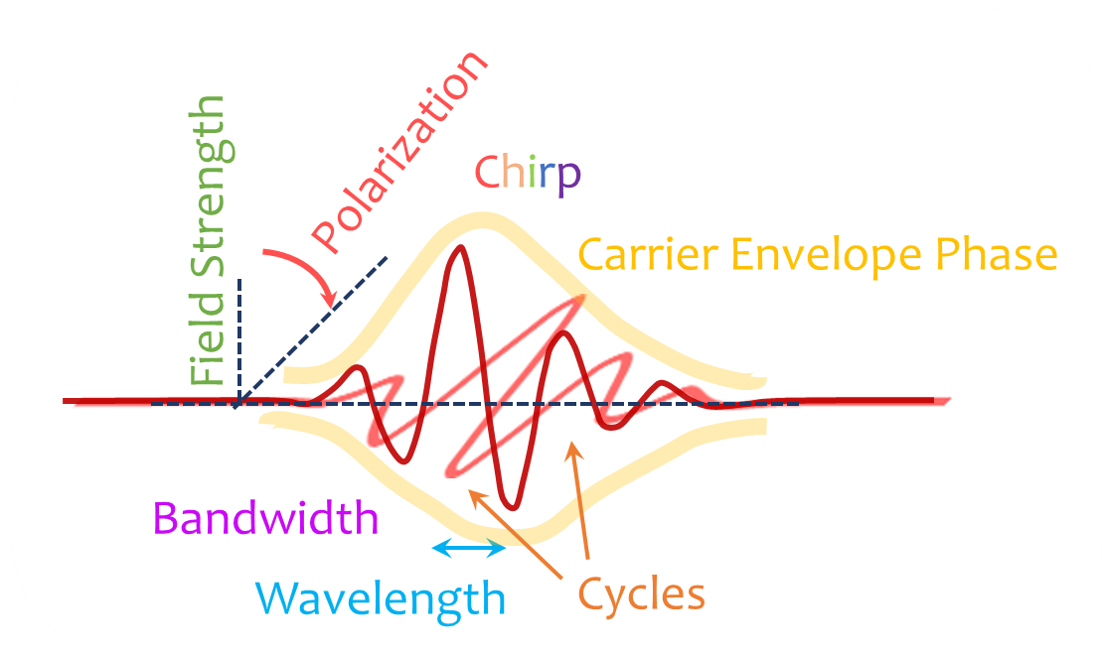
Time-domain THz spectroscopy is a spectroscopic technique that can provide the complete, complex optical response of materials, without requiring a broadband spectrum and Kramers-Kronig transformation. This is because the full phase and amplitude information of a CEP-stable THz field (rather than the intensity alone) is captured using electro-optic sampling.
Learn more about THz generation and detection techniques below.
Generating broadband THz pulses
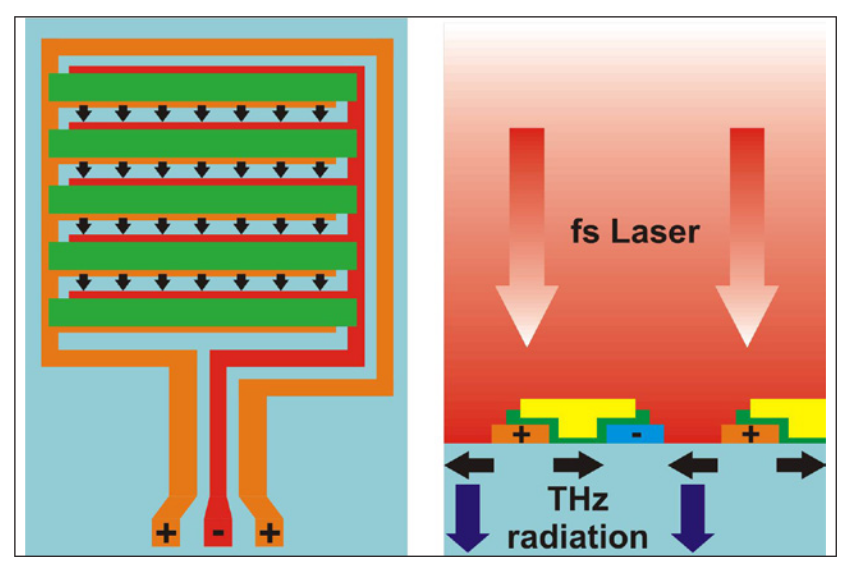
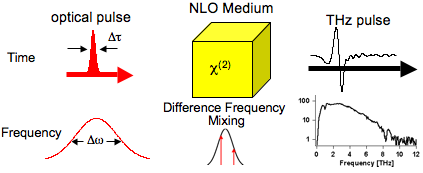
Broadband THz pulses are useful as probe of a material's optical response. Pulses can be generated in three ways: optical rectification in a nonlinear crystal, photoconductive switches, and laser-ionized plasma.
Optical rectification with nonlinear crystals can produce broadband spectrums from 0.5 THz up to, for example, 2.5 THz in ZnTe or even up to 100 THz in GaSe. Other popular nonlinear crystals include GaP and organic materials such as DAST, which can produce spectrums between 0.1-10 THz. The range depends on the polarization and incidence angle of the near-infrared (NIR) pulses with respect to the nonlinear medium, the NIR pulse duration, and phase matching between the incoming and THz light.
There are several methods for plasma generation. The two color plasma scheme uses tunnel ionization to accelerate electrons in a laser field, releasing broadband radiation with no sharp absorption lines. This generation scheme works by passing an 800 nm beam through a nonlinear crystal (generally, BBO) to generate second harmonic light at 400 nm. The remaining co-propagating 800 nm beam and the 400 nm beam are focused in air to create a volume with a fluence beyond the ionization threshold of the air. Mixing with the 2nd harmonic light introduces an asymmetry in the electric field, which accelerates the ionized electrons and produces THz radiation.
Electro-optic sampling
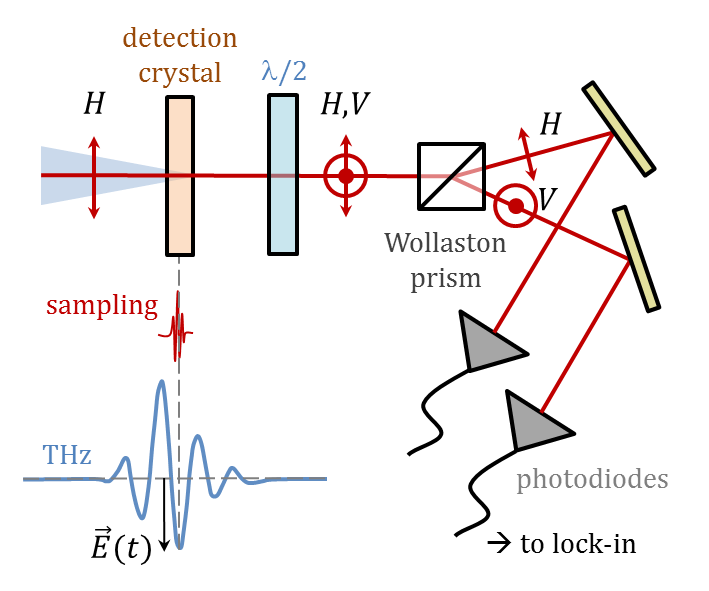
The general procedure involves the use of an optical pulse with a duration much shorter than that of the THz field to sample the field profile. (In practice, a beam-splitter reserves a fraction of the femtosecond laser beam that is used to generate the THz in order to sample the resulting pulse.) The THz field interacts with the sampling beam in a nonlinear crystal via the Pockels effect, in which the electric field due to the THz pulse generates birefringence proportional to the field strength. This birefringence leads to a rotation of the polarization of the sampling beam linearly proportional to the amplitude of the part of the THz spectrum that is impinging on the nonlinear crystal. The polarization of the sampling beam is then recorded. Iterative measurements, shifting the timing of the short sampling pulse to coincide with different parts of the longer THz pulse, allow the recovery of the full spectrum.
An electro-optic sampling (EOS) scheme is depicted above, at right. The sampling beam is initially polarized such that, in the absence of an applied field, a Wollaston prism will split the beam into two pulses of equal intensity but opposing polarization. These pulses are detected in two photodiodes, whose signals are subtracted. This "balanced detection" scheme ensures that whatever net signal is detected reflects the polarization imbalance produced by the THz field. A linear polarization scheme is depicted here, where a half- or quarter-wave (λ/2 or λ/4) plate rotates the sampling beam. Circularly polarized schemes are also frequently used.
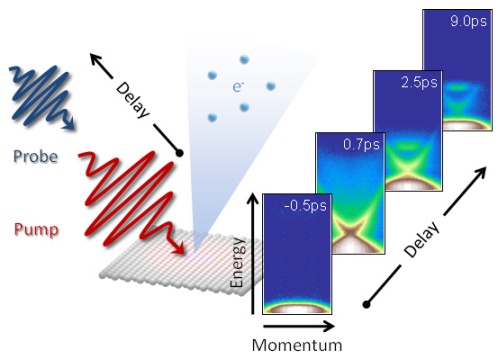
Pump-probe spectroscopy
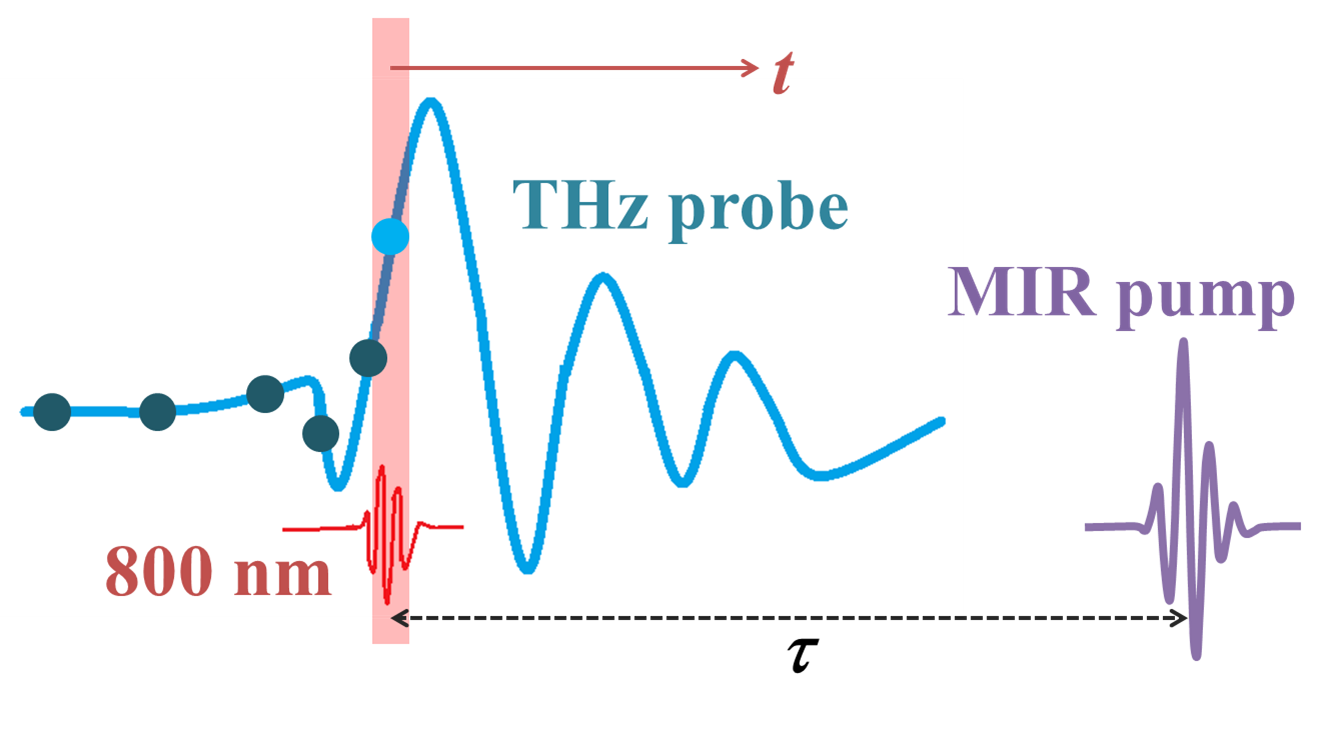
This is because the THz profile that is measured is not simply the profile of the reflected/transmitted THz beam some time delay after pump excitation. The profile at a given time delay τ after excitation is actually comprised from a series of measurements, with each part of the THz spectrum measured with the sampling beam delay fixed at τ time from the pump beam. The result is an "instantaneous" representation of the sample response at time τ after excitation.
From THz spectrum to optical response
Extracting the absolute optical response requires two measurements, (1) the THz pulse reflected or transmitted from the sample of interest, and (2) a reference THz measurement from a material whose full response is known. These should be measured in identical conditions, ideally in sequence or simultaneously. This is the same requirement in principle as for Fourier transform infrared spectroscopy (FTIR), ellipsometry, and similar techniques for optical characterization. The key difference is that since time-domain THz spectroscopy captures both amplitude and phase information of the sample and reference, a narrow spectrum is sufficient to determine the complex response.
For multilayer materials, modeling the system is required to back out the contribution of each material to the total measured response. Similarly, if a pump excites a smaller volume fraction of the system than the THz probe (due to a mismatch in the penetration depth of the light at each wavelength), modeling can be used isolate the response of the excited volume alone. Methods for how to do this, along with relevant references, are discussed in my thesis.