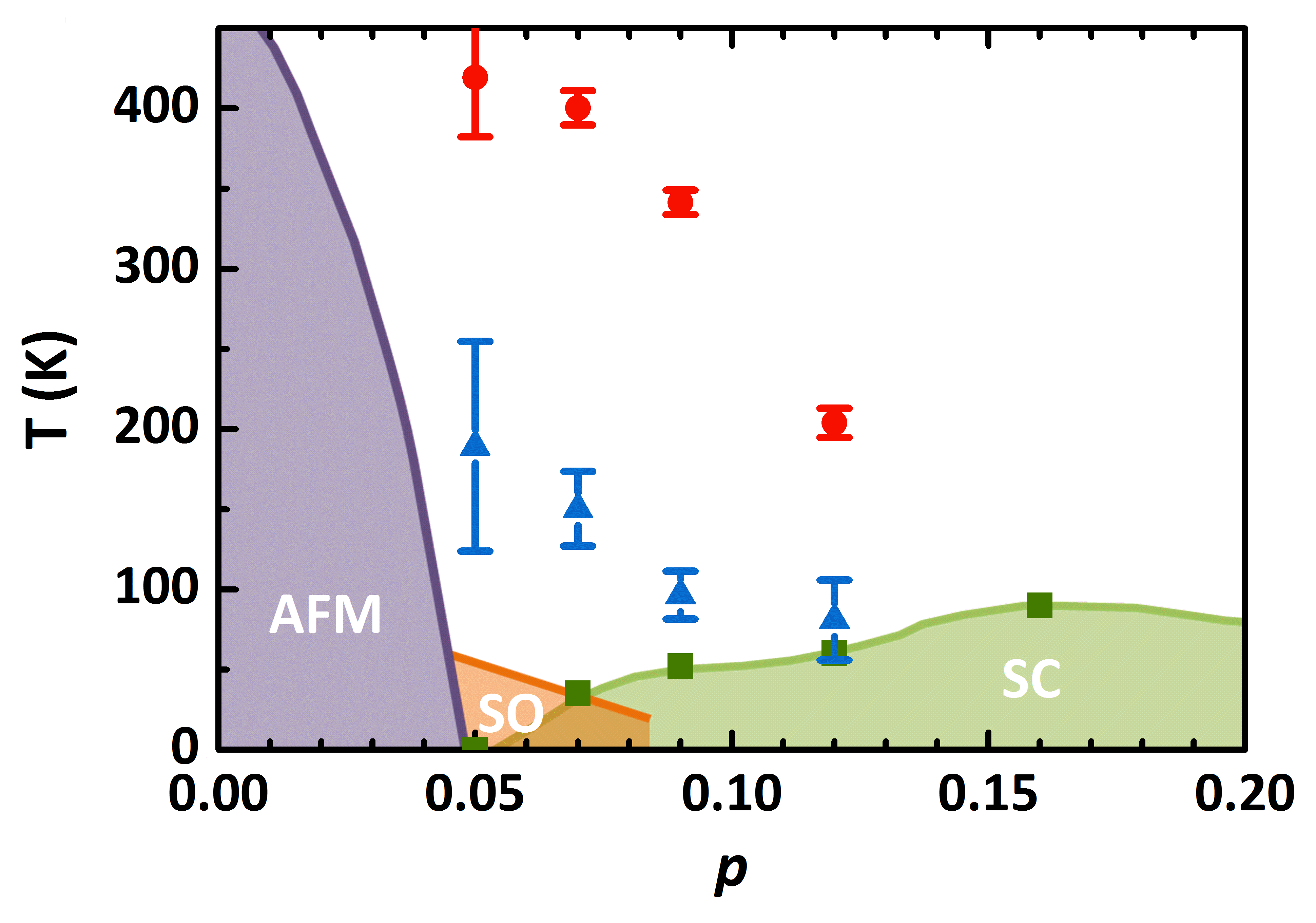
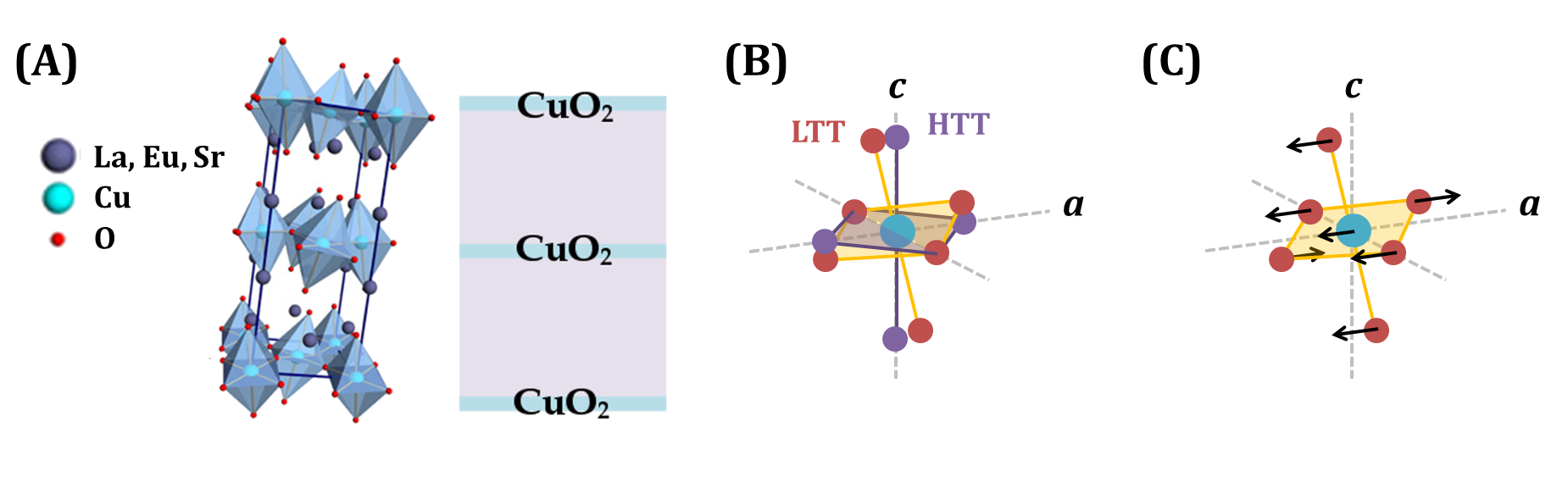
Manipulating phase competition in La1.8-xEu0.2SrxCuO4
The key to restoring superconducting coupling was to tilt the energetic balance against charge ordering by preferentially destroying stripes without introducing quasiparticle excitations that would break superconducting pairing. An Eu-symmetric phonon mode associated with the stretching of the Cu-O bonds was chosen with the aim to disrupt the stripe synchronicity with the lattice. After the first experiments on LESCO, it was shown that in related compound La1.875Ba0.125CuO4 (LBCO 1/8) that this excitation does in fact promptly reduce charge stripe order, on the same timescale that superconducting coupling is restored in LESCO.
Restoring intrinsic superconducting tunneling
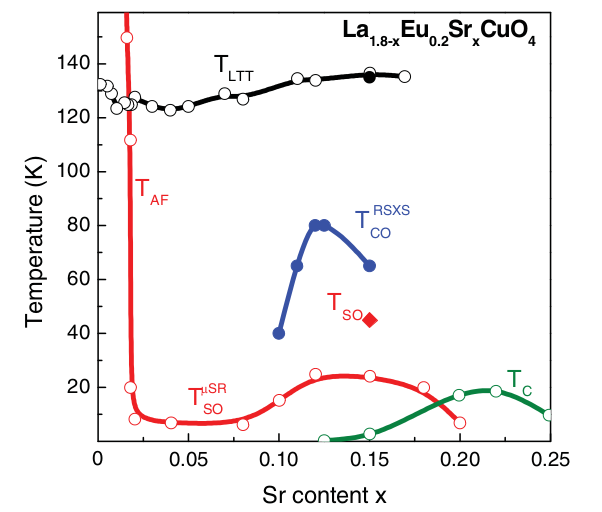
A single crystal of LESCO 1/8 was excited using light pulses polarized along the crystallographic a-axis and made resonant to the 15 μm Eu mode. The time-resolved light-induced optical response was measured using time-domain THz spectroscopy. The optical fingerprint for superconducting coupling in cuprates is the Josephson plasma resonance, a mode that arises due to intrinsic Josephson coupling between CuO2 planes. In a first series of measurements performed before I joined the Cavalleri group, a light-induced plasma mode was generated with a plasma frequency similar to that of the Josephson mode in related superconducting lanthanides. This transient plasma mode was detected up to 10-20 K, in the regime where both spins and charges order.
With improved experimental apparatus and a four-fold increase in pump fluence, I was able to detect this coupling up to higher temperatures, discovering that it persists throughout the charge ordered regime--up to 80 K, well above the highest Tc of any lanthanide cuprate.
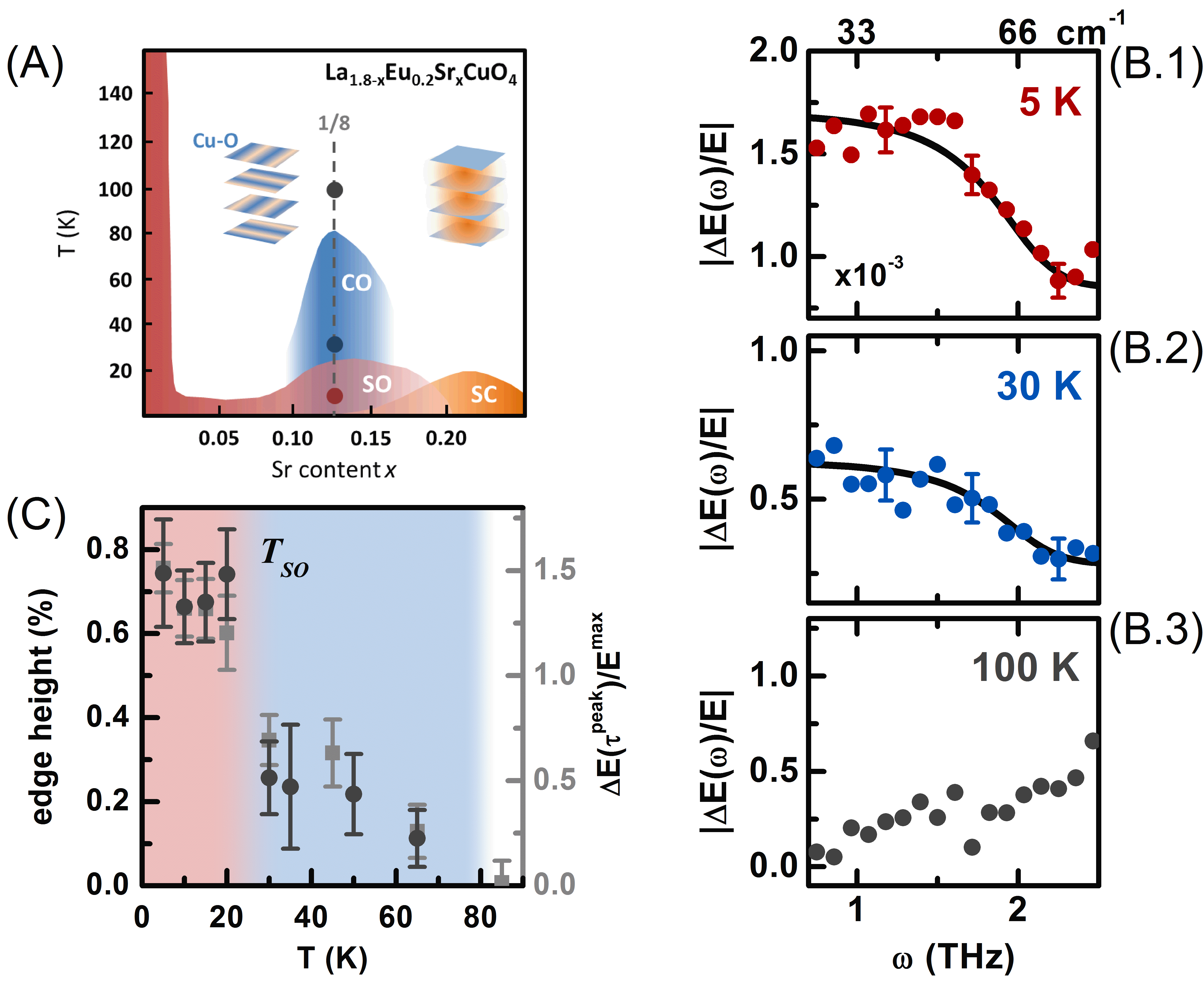
Decoherence-driven relaxation
The relaxation pathway of the light-induced plasma mode offers further compelling evidence that the feature is related to Josephson coupling. From the reflected THz field, we extracted the full complex optical response as a function of delay time after excitation. The response was well-fit by a Drude picture of a single plasma mode. Importantly, the relaxation of the light-induced plasma mode is dominated by a collapse of the coherence length of the plasma (related to the effective scattering rate in the Drude picture), rather than by a reduction in its density (ie, the plasma frequency). This is in contrast to what is measured from excited quasiparticles, which decay by a loss in carrier density at either constant or decreasing scattering.
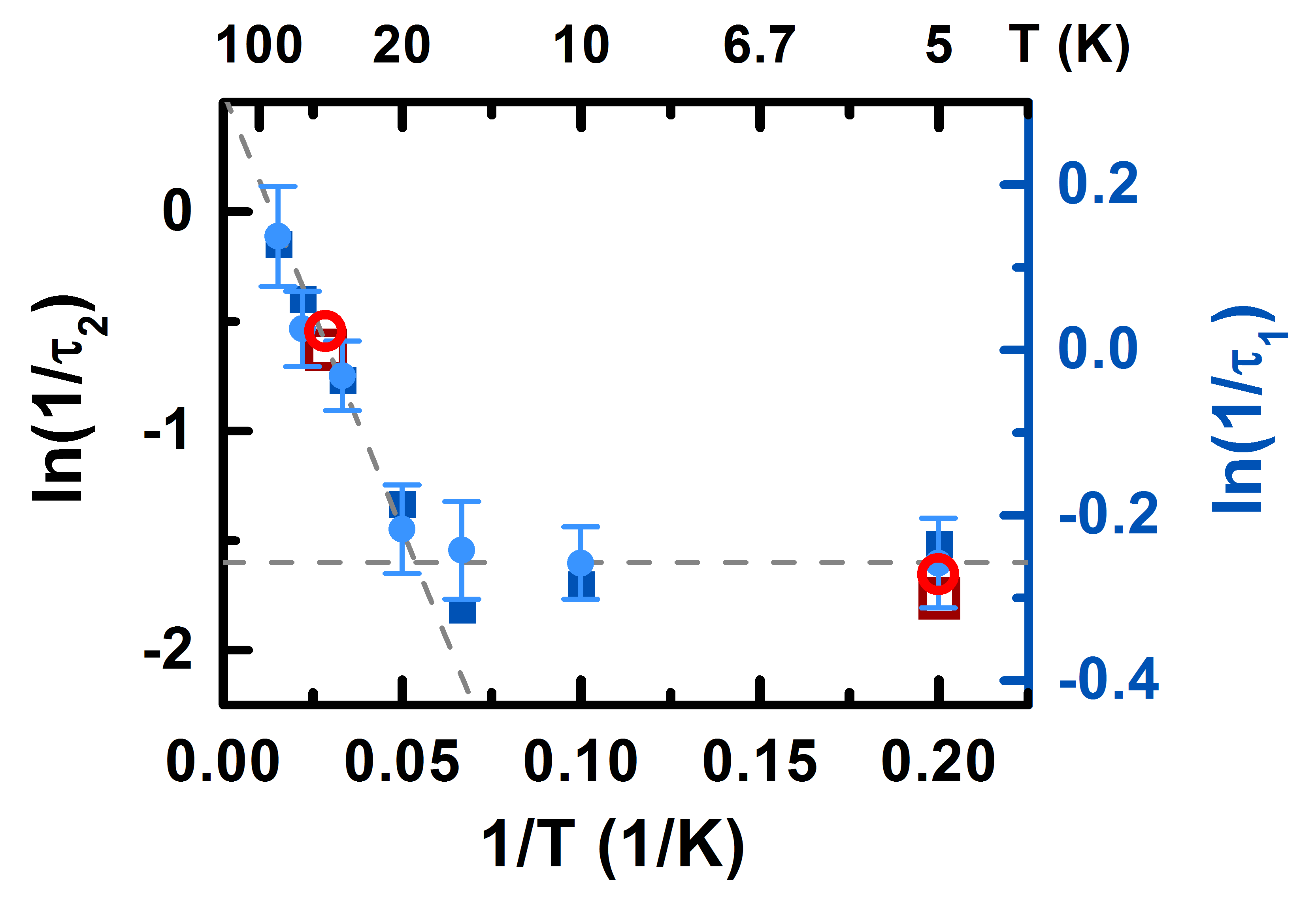
The departure from activated behavior below TSO may therefore be related to the freezing out of spin fluctuations. A temperature-independent relaxation rate would be compatible with quantum coherent tunneling between two states, for instance between superconducting and "pair density wave" phases at constant carrier density.
Charge order mingles with superconductivity?
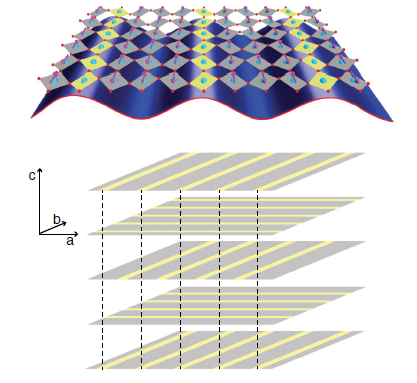
The proposed pair-density wave state is one example of "intertwined order," in which multiple orders interact to determine the complex behavior of a material. A similar type of multi-component order parameter that encompasses both charge density wave and superconducting states has been described to model the entire cuprate pseudogap.
Publications associated with this research
"Two distinct kinetic regimes for the relaxation of light-induced superconductivity in La1.675Eu0.2Sr0.125CuO4,"
C. R. Hunt, D. Nicoletti, S. Kaiser, T. Takayama, H. Takagi, and A. Cavalleri.
Phys. Rev. B 91, 020505(R) (2015). Rapid Communication Editor's Suggestion arXiv
"Melting of charge stripes in vibrationally driven La1.875Ba0.125CuO4: Assessing the respective roles of electronic and lattice order in frustrated superconductors,"
M. Först, et al.
Phys. Rev. Lett. 112, 157002 (2014). arXiv
"Light-induced superconductivity in a stripe-order cuprate,"
D. Fausti, R. I. Tobey, et al.